1560. Decreasing Number

There are three types of operations that can be performed on an integer:

· If the number is divisible by 3, divide it by 3;

· If the number is divisible by 2, divide it by 2;

· Subtract 1.

For a given positive integer n, find the minimum number of operations required to obtain 1.

Input. Each line contains a single positive integer n (1 ≤ n ≤ 10⁶).

Output. For each value of n, print the minimum number of operations required to obtain 1 on a separate line.

Sample input	Sample output
1 5 10	0 3 3

SOLUTION

dynamic programming

Algorithm analysis

Let f(n) represent the minimum number of operations required to transform the number n into 1. For example,

· f(1) = 0, as we already have the number 1;

· f(2) = 1, perform operation 2 → 1;

· f(5) = 3, perform operations 5 → 4 → 2 → 1;

· f(10) = 3, perform operations 10 → 9 → 3 → 1;

In the case of n = 10, it is more advantageous to subtract 1 first rather than using the greedy approach and dividing by 2.

Let’s consider the process of computing the function f(n).

· If we divide the number n by 3 (assuming n is divisible by 3), then

f(n) = f(n / 3) + 1

· If we divide the number n by 2 (assuming n is divisible by 2), then

f(n) = f(n / 2) + 1

· If we subtract 1 from the number n, then

f(n) = f(n – 1) + 1

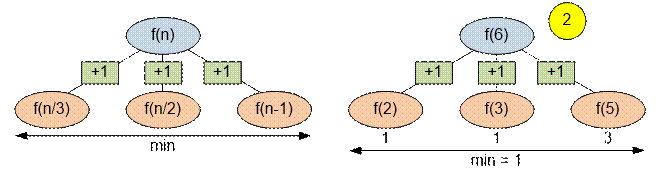
From the number n, we can obtain one of three numbers: n / 3, n / 2, or n – 1. The number of operations required to reduce each of these numbers to 1, is equal to f(n / 3), f(n / 2), and f(i – 1) respectively. Since we are interested in the minimum number of operations, we have the following relationship:

f(n) = min(f(n – 1), f(n / 2), f(n / 3)) + 1,

f(1) = 0

In the case, if n is not divisible by 2 (or by 3), then the corresponding element (f(n / 2) or f(n / 3)) is absent in the min function. For example, for n = 8, we have:

f(8) = min(f(7), f(4)) + 1

Similarly, for n = 7, we get:

f(7) = min(f(6)) + 1 = f(6) + 1

The values of the function f(n) will be stored in the cells of the array d[MAX], where MAX = 10⁶ + 1. Fill the cells of the array d from 1 to 10⁶ according to the given recurrence relation. For example, the following table shows the values of d[i] for 1 £ i £ 11:

For example,

d[10] = min(d[9], d[5]) + 1 = min(2, 3) + 1 = 3

In other words, it is more efficient to subtract 1 from 10, rather than divide it by 2.

Exercise

Find the values of d[i] for the following values of i:

Algorithm realization

Declare an array d, where the i-th cell contains the minimum number of operations required to transform the number i into 1.

int d[1000001];

Fill the cells of array d according to the provided formulas.

d[1] = 0;

for(i = 2; i <= 1000000; i++)

{

// d[i] = min(d[i/3],d[i/2],d[i-1]) + 1

d[i] = d[i-1];

if (i % 2 == 0 && d[i/2] < d[i]) d[i] = d[i/2];

if (i % 3 == 0 && d[i/3] < d[i]) d[i] = d[i/3];

d[i]++;

}

For each input value n, print the answer d[n].

while(scanf("%d",&n) == 1)

printf("%d\n",d[n]);

Algorithm realization – recursion

#include <stdio.h>

#include <string.h>

#define INF 2000000000

int i, res, n;

int dp[1000001];

int min(int a, int b, int c)

{

int res = a;

if (b < res) res = b;

if (c < res) res = c;

return res;

}

int f(int n)

{

if (n == 1) return 0;

if (dp[n] != -1) return dp[n];

int a = f(n - 1);

int b = (n % 2 == 0) ? f(n / 2) : INF;

int c = (n % 3 == 0) ? f(n / 3) : INF;

return dp[n] = min(a,b,c) + 1;

}

int main(void)

{

memset(dp, -1, sizeof(dp));

while (scanf("%d", &n) == 1)

{

res = f(n);

printf("%d\n", res);

}

return 0;

}

Java realization

import java.util.*;

public class Main

{

public static int MAX = 1000001;

static int d[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

d[1] = 0;

for(int i = 2; i < MAX; i++)

{

d[i] = d[i-1] + 1;

if (i % 2 == 0) d[i] = Math.min(d[i], d[i/2] + 1);

if (i % 3 == 0) d[i] = Math.min(d[i], d[i/3] + 1);

}

while(con.hasNext())

{

int n = con.nextInt();

System.out.println(d[n]);

}

}

}

Python realization

Create a list d, where the i-th cell contains the minimum number of operations required to transform the number i into 1.

d = [0] * 1000001

Fill the cells of array d according to the provided formulas.

d[1] = 0

for i in range(2, 1000001):

d[i] = d[i - 1]

if i % 2 == 0 and d[i // 2] < d[i]:

d[i] = d[i // 2]

if i % 3 == 0 and d[i // 3] < d[i]:

d[i] = d[i // 3]

d[i] += 1

For each input value n, print the answer d[n].

while True:

try:

n = int(input())

print(d[n])

except EOFError:

break